How To Find The Exponential Function Given Two Points Calculator

Exponential Functions

In this section, you will:

• Evaluate exponential functions.
• Find the equation of an exponential part.
• Use chemical compound involvement formulas.
• Evaluate exponential functions with base $\mathrm{eastward}$

  .

India is the second most populous country in the world with a population of most$1.25$

billion people in 2013. The population is growing at a rate of about$\mathrm{1.two}\%$

each year^one. If this rate continues, the population of India will exceed China's population past the year$2031.$

When populations abound rapidly, we often say that the growth is "exponential," meaning that something is growing very rapidly. To a mathematician, nevertheless, the term exponential growth has a very specific meaning. In this section, nosotros will have a await at exponential functions, which model this kind of rapid growth.

Identifying Exponential Functions

When exploring linear growth, we observed a constant rate of change—a constant number by which the output increased for each unit increase in input. For instance, in the equation$f(x)=3\mathrm{10}+\mathrm{iv},$

the slope tells us the output increases by iii each fourth dimension the input increases by 1. The scenario in the India population example is different because nosotros have a per centum change per unit time (rather than a constant alter) in the number of people.

Defining an Exponential Part

A study found that the percent of the population who are vegans in the U.s.a. doubled from 2009 to 2011. In 2011, ii.5% of the population was vegan, adhering to a diet that does not include any animal products—no meat, poultry, fish, dairy, or eggs. If this rate continues, vegans will brand upward ten% of the U.South. population in 2015, 40% in 2019, and eighty% in 2021.

What exactly does it mean to grow exponentially? What does the word double take in common with percent increase? People toss these words around errantly. Are these words used correctly? The words certainly appear oftentimes in the media.

• Percent modify refers to a change based on a percent of the original amount.
• Exponential growth refers to an increase based on a abiding multiplicative rate of change over equal increments of time, that is, a percent increase of the original amount over time.
• Exponential disuse refers to a subtract based on a constant multiplicative rate of modify over equal increments of time, that is, a percent decrease of the original amount over fourth dimension.

For us to proceeds a clear understanding of exponential growth, permit united states contrast exponential growth with linear growth. Nosotros will construct two functions. The first function is exponential. We will start with an input of 0, and increase each input by 1. Nosotros volition double the corresponding consecutive outputs. The second role is linear. We volition start with an input of 0, and increase each input by 1. Nosotros will add 2 to the respective consecutive outputs. Come across [link].

0	1	0
1	ii	2
2	iv	iv
3	8	half-dozen
4	16	eight
5	32	x
6	64	12

From [link] we tin can infer that for these two functions, exponential growth dwarfs linear growth.

• Exponential growth refers to the original value from the range increases by the aforementioned percent over equal increments found in the domain.
• Linear growth refers to the original value from the range increases past the same amount over equal increments found in the domain.

Manifestly, the difference betwixt "the same percentage" and "the aforementioned amount" is quite meaning. For exponential growth, over equal increments, the constant multiplicative rate of modify resulted in doubling the output whenever the input increased by one. For linear growth, the constant additive rate of modify over equal increments resulted in calculation 2 to the output whenever the input was increased past one.

The general form of the exponential function is$f(\mathrm{ten})=a{b}^x,$

where$a$

is any nonzero number,$b$

is a positive real number not equal to ane.

• If $b>1,$

  the function grows at a charge per unit proportional to its size.

• If $0<b<1,$

  the function decays at a charge per unit proportional to its size.

Permit's look at the function$f(x)={\mathrm{ii}}^x$

from our example. We will create a table ([link]) to decide the respective outputs over an interval in the domain from$-3$

to$3.$

| $$

x

</math></strong> | $-\mathrm{iii}$

| | $$

f ( x ) = 2 x

</math></strong> | ${\mathrm{two}}^{-\mathrm{iii}}=\frac{\mathrm{one}}{\mathrm{eight}}$

Let us examine the graph of$f$

by plotting the ordered pairs we discover on the table in [link], and then make a few observations.

Let'due south define the behavior of the graph of the exponential role$f(\mathrm{ten})={\mathrm{ii}}^{\mathrm{10}}$

and highlight some its central characteristics.

• the domain is $\left(-\infty ,\infty \right),$
• the range is $\left(0,\infty \right),$
• as $x\to \infty ,f(x)\to \infty ,$
• as $x\to -\infty ,f(\mathrm{10})\to 0,$
• $f(x)$

  is always increasing,

• the graph of $f(x)$

  volition never bear upon the x-axis because base two raised to any exponent never has the result of zero.

• $y=0$

  is the horizontal asymptote.

• the y-intercept is 1.

Exponential Part

For any real number$x,$

an exponential function is a part with the form

$f(x)=a{b}^{\mathrm{10}}$

where

• $a$

  is a non-zero real number chosen the initial value and

• $b$

  is any positive real number such that

  $b\ne 1.$
• The domain of $f$

  is all existent numbers.

• The range of $f$

  is all positive real numbers if

  $a>0.$
• The range of $f$

  is all negative real numbers if

  $a<0.$
• The y-intercept is $\left(0,a\right),$

  and the horizontal asymptote is

  $y=0.$

Identifying Exponential Functions

Which of the following equations are not exponential functions?

• $f(x)={\mathrm{iv}}^{3\left(x-\mathrm{two}\right)}$
• $\mathrm{chiliad}(\mathrm{10})=x^3$
• $h(\mathrm{ten})={\left(\frac{\mathrm{i}}{3}\right)}^x$
• $j(x)={\left(-2\right)}^x$

By definition, an exponential function has a constant as a base of operations and an independent variable equally an exponent. Thus,$\mathrm{grand}(\mathrm{ten})={\mathrm{10}}^{\mathrm{three}}$

does not represent an exponential part because the base is an independent variable. In fact,$g(x)=x^3$

is a power function.

Recall that the base b of an exponential part is ever a positive constant, and$b\ne 1.$

Thus,$j(x)={\left(\mathrm{-ii}\right)}^x$

does not represent an exponential part because the base,$\mathrm{-2},$

is less than$0.$

Which of the following equations stand for exponential functions?

• $f(x)=2{\mathrm{10}}^{\mathrm{ii}}-\mathrm{three}x+1$
• $\mathrm{one\; thousand}(x)={0.875}^{\mathrm{ten}}$
• $h(\mathrm{10})=\mathrm{ane.75}\mathrm{10}+2$
• $j(\mathrm{ten})={1095.6}^{-2x}$

$\mathrm{one\; thousand}(x)={0.875}^x$

and$j(x)={\mathrm{1095.half\; dozen}}^{-\mathrm{two}x}$

correspond exponential functions.

Evaluating Exponential Functions

Call back that the base of operations of an exponential function must be a positive real number other than$\mathrm{one.}$

Why practise we limit the base of operations $b$

to positive values? To ensure that the outputs will exist existent numbers. Find what happens if the base is non positive:

• Let $b=-9$

  and

  $x=\frac{\mathrm{one}}{\mathrm{two}}.$

  Then

  $f(x)=f\left(\frac{\mathrm{ane}}{\mathrm{two}}\right)={\left(-9\right)}^{\frac{\mathrm{ane}}{2}}=\sqrt{-9},$

  which is not a real number.

Why do we limit the base to positive values other than $\mathrm{one}?$

Considering base $1$

results in the constant function. Detect what happens if the base is $1:$

• Permit $b=\mathrm{i.}$

  So

  $f(x)=1^x=1$

  for any value of

  $\mathrm{ten}.$

To evaluate an exponential part with the class$f(x)=b^x,$

we just substitute $x$

with the given value, and summate the resulting power. For example:

Let $f(x)={\mathrm{ii}}^x.$

What is $f(\mathrm{iii})?$

$$\begin{array}{lll}f\left(x\right)\hfill & ={\mathrm{two}}^x\hfill & \hfill \\ f\left(\mathrm{iii}\right)\hfill & ={\mathrm{ii}}^{\mathrm{iii}}\hfill & \text{Substitute}\mathrm{10}=3.\hfill \\ \hfill & =8\hfill & \text{Evaluate the power}\text{.}\hfill \end{array}$$

To evaluate an exponential part with a course other than the bones form, it is important to follow the social club of operations. For example:

Allow$f(x)=30{\left(\mathrm{ii}\right)}^{\mathrm{ten}}.$

What is$f(\mathrm{three})?$

$$\begin{array}{lll}f\left(x\right)\hfill & =30{\left(2\right)}^x\hfill & \hfill \\ f\left(\mathrm{iii}\right)\hfill & =30{\left(2\right)}^3\hfill & \text{Substitute}\mathrm{ten}=\mathrm{three.}\hfill \\ \hfill & =\mathrm{xxx}\left(\mathrm{eight}\right)\hfill & \text{Simplify the power beginning}\text{.}\hfill \\ \hfill & =240\hfill & \text{Multiply}\text{.}\hfill \end{array}$$

Notation that if the order of operations were not followed, the issue would exist incorrect:

$$f(3)=30{\left(2\right)}^3\ne {60}^3=\mathrm{216,000}$$

Evaluating Exponential Functions

Permit $f\left(\mathrm{10}\right)=5{\left(3\right)}^{\mathrm{ten}+1}.$

Evaluate$f\left(2\right)$

without using a reckoner.

Follow the order of operations. Be sure to pay attending to the parentheses.

$$\begin{array}{lll}f\left(\mathrm{10}\right)\hfill & =5{\left(3\right)}^{x+\mathrm{one}}\hfill & \hfill \\ f\left(2\right)\hfill & =5{\left(\mathrm{three}\right)}^{2+\mathrm{i}}\hfill & \text{Substitute}x=2.\hfill \\ \hfill & =\mathrm{v}{\left(\mathrm{three}\right)}^{\mathrm{iii}}\hfill & \text{Add the exponents}.\hfill \\ \hfill & =\mathrm{five}\left(27\right)\hfill & \text{Simplify the power}\text{.}\hfill \\ \hfill & =135\hfill & \text{Multiply}\text{.}\hfill \end{array}$$

Let$f\left(x\right)=8{\left(\mathrm{i.ii}\right)}^{x-\mathrm{five}}.$

Evaluate$f\left(\mathrm{three}\right)$

using a estimator. Round to four decimal places.

$5.5556$

Defining Exponential Growth

Because the output of exponential functions increases very rapidly, the term "exponential growth" is often used in everyday language to describe anything that grows or increases apace. Yet, exponential growth can be defined more precisely in a mathematical sense. If the growth rate is proportional to the amount present, the function models exponential growth.

Exponential Growth

A role that models exponential growth grows by a rate proportional to the corporeality present. For whatever existent number$x$

and whatsoever positive real numbers$a$

and$b$

such that$b\ne \mathrm{i},$

an exponential growth function has the form

$f(x)=a{b}^{\mathrm{ten}}$

where

• $a$

  is the initial or starting value of the role.

• $b$

  is the growth gene or growth multiplier per unit

  $x$

  .

In more general terms, we accept an exponential office, in which a abiding base is raised to a variable exponent. To differentiate between linear and exponential functions, let's consider two companies, A and B. Visitor A has 100 stores and expands by opening 50 new stores a yr, so its growth can be represented by the function$A\left(\mathrm{ten}\right)=100+50x.$

Company B has 100 stores and expands by increasing the number of stores by 50% each yr, so its growth can be represented by the function $B(x)=100{\left(1+0.5\right)}^x.$

A few years of growth for these companies are illustrated in [link].

Stores, Company A	Stores, Visitor B
$0$

The graphs comparison the number of stores for each company over a v-year period are shown in [link]. We can see that, with exponential growth, the number of stores increases much more than rapidly than with linear growth.

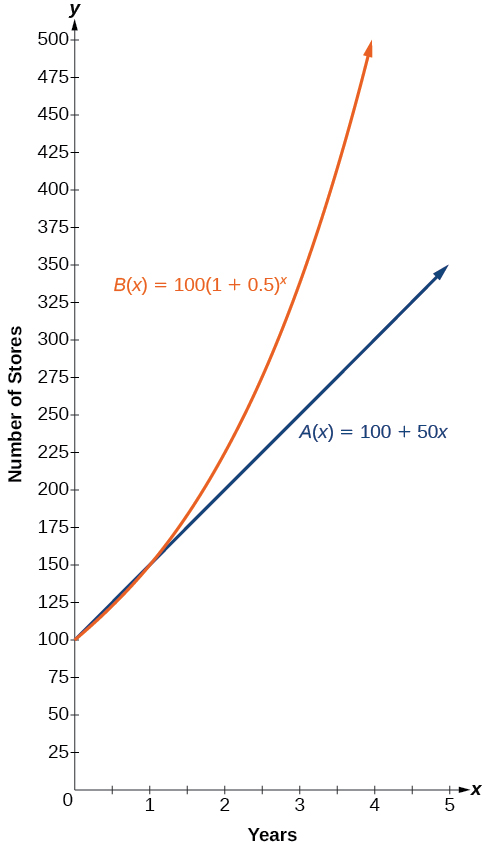
Notice that the domain for both functions is$[0,\infty ),$

and the range for both functions is$[100,\infty ).$

Later on twelvemonth one, Company B always has more stores than Company A.

Now we volition turn our attending to the function representing the number of stores for Company B,$B(x)=100{\left(\mathrm{ane}+0.5\right)}^x.$

In this exponential function, 100 represents the initial number of stores, 0.50 represents the growth charge per unit, and$1+0.5=\mathrm{ane.5}$

represents the growth factor. Generalizing further, nosotros can write this role equally$B(\mathrm{ten})=100{\left(1.5\right)}^x,$

where 100 is the initial value,$\mathrm{one.5}$

is chosen the base, and$x$

is chosen the exponent.

Evaluating a Real-World Exponential Model

At the showtime of this section, we learned that the population of Republic of india was about$1.25$

billion in the yr 2013, with an annual growth rate of about$\mathrm{i.2}\%.$

This situation is represented by the growth function$P(t)=1.25{\left(1.012\right)}^t,$

where $t$

is the number of years since$2013.$

To the nearest thousandth, what volition the population of India be in$\text{2031?}$

To estimate the population in 2031, we evaluate the models for$t=18,$

because 2031 is$\mathrm{eighteen}$

years after 2013. Rounding to the nearest thousandth,

$$P(18)=\mathrm{one.25}{\left(\mathrm{ane.012}\right)}^{18}\approx 1.549$$

There volition be about 1.549 billion people in Republic of india in the twelvemonth 2031.

The population of Mainland china was about ane.39 billion in the year 2013, with an annual growth rate of about$0.6\%.$

This situation is represented by the growth function$P(t)=1.39{\left(\mathrm{ane.006}\right)}^t,$

where $t$

is the number of years since$2013.$

To the nearest thousandth, what volition the population of Cathay exist for the twelvemonth 2031? How does this compare to the population prediction we made for Republic of india in [link]?

About$1.548$

billion people; past the yr 2031, India'due south population will exceed Mainland china's by about 0.001 billion, or 1 1000000 people.

Finding Equations of Exponential Functions

In the previous examples, we were given an exponential part, which nosotros then evaluated for a given input. Sometimes nosotros are given data almost an exponential function without knowing the function explicitly. We must apply the data to first write the form of the function, and so decide the constants$a$

and$b,$

and evaluate the part.

Given two data points, write an exponential model.

1. If i of the data points has the class $\left(0,a\right),$

   and then

   $a$

   is the initial value. Using

   $a,$

   substitute the second point into the equation

   $f(x)=a{\left(b\right)}^x,$

   and solve for

   $b.$
2. If neither of the data points have the form $\left(0,a\right),$

   substitute both points into two equations with the grade

   $f(x)=a{\left(b\right)}^{\mathrm{10}}.$

   Solve the resulting system of two equations in two unknowns to observe

   $a$

   and

   $b.$
3. Using the $a$

   and

   $b$

   found in the steps in a higher place, write the exponential function in the form

   $f(\mathrm{ten})=a{\left(b\right)}^x.$

Writing an Exponential Model When the Initial Value Is Known

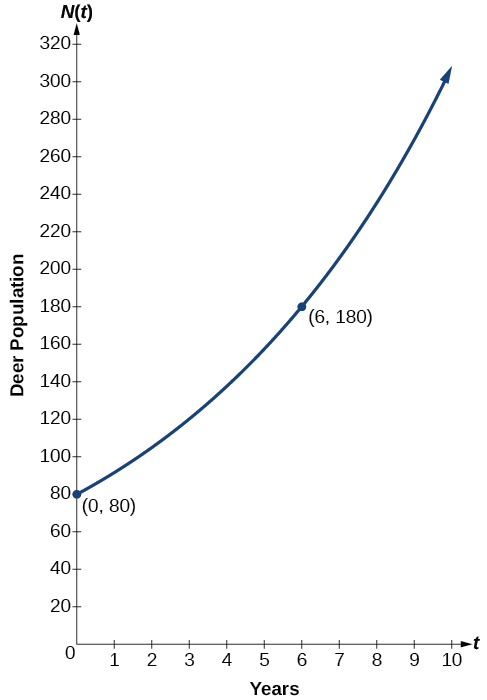
In 2006, 80 deer were introduced into a wild animals refuge. By 2012, the population had grown to 180 deer. The population was growing exponentially. Write an algebraic office$N(t)$

representing the population$\left(N\right)$

of deer over time$t.$

We let our independent variable$t$

be the number of years after 2006. Thus, the information given in the problem tin exist written as input-output pairs: (0, 80) and (6, 180). Notice that past choosing our input variable to be measured as years after 2006, we take given ourselves the initial value for the function,$a=\mathrm{lxxx.}$

We can now substitute the second point into the equation$\mathrm{Due\; north}(t)=80b^t$

to detect$b:$

$$\begin{array}{lll}N(t)\hfill & =\mathrm{lxxx}{b}^t\hfill & \hfill \\ 180\hfill & =80b^{\mathrm{vi}}\hfill & \text{Substitute using indicate}(\mathrm{vi},180).\hfill \\ \frac{\mathrm{nine}}{4}\hfill & =b^{\mathrm{six}}\hfill & \text{Divide and write in lowest terms}.\hfill \\ b\hfill & ={\left(\frac{9}{4}\right)}^{\frac{1}{6}}\hfill & \text{Isolate}b\text{ using properties of exponents}.\hfill \\ b\hfill & \approx \mathrm{one.1447}\begin{array}{cccc}& & & \end{array}\hfill & \text{Round to 4 decimal places}.\hfill \end{array}$$

Note: Unless otherwise stated, exercise not round any intermediate calculations. So round the last answer to four places for the residue of this section.

The exponential model for the population of deer is$\mathrm{North}(t)=\mathrm{eighty}{\left(1.1447\right)}^t.$

(Notation that this exponential function models brusque-term growth. Equally the inputs gets large, the output will become increasingly larger, so much so that the model may not be useful in the long term.)

We can graph our model to observe the population growth of deer in the refuge over time. Discover that the graph in [link] passes through the initial points given in the problem,$\left(0,\text{ eight}0\right)$

and$\left(\text{6},\text{ xviii}0\right).$

We tin as well encounter that the domain for the function is$[0,\infty ),$

and the range for the office is$[80,\infty ).$

A wolf population is growing exponentially. In 2011,$129$

wolves were counted. Past$\text{2013,}$

the population had reached 236 wolves. What two points tin can be used to derive an exponential equation modeling this situation? Write the equation representing the population$N$

of wolves over time$t.$

$\left(0,129\right)$

and$\left(2,236\right);N(t)=129{\left(\text{1}\text{.3526}\right)}^t$

Writing an Exponential Model When the Initial Value is Not Known

Find an exponential function that passes through the points$\left(-2,6\right)$

and$\left(\mathrm{ii},\mathrm{ane}\right).$

Because we don't have the initial value, we substitute both points into an equation of the course$f(x)=a{b}^{\mathrm{ten}},$

and so solve the organization for$a$

and$b.$

• Substituting $\left(-\mathrm{ii},\mathrm{half-dozen}\right)$

  gives

  $\mathrm{half-dozen}=a{b}^{-\mathrm{ii}}$
• Substituting $\left(\mathrm{ii},1\right)$

  gives

  $1=a{b}^2$

Utilize the first equation to solve for$a$

in terms of$b:$

---

Substitute$a$

in the second equation, and solve for$b:$

Employ the value of$b$

in the first equation to solve for the value of$a:$

---

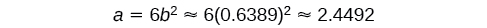Thus, the equation is$f(x)=2.4492{(0.6389)}^x.$

We can graph our model to check our work. Notice that the graph in [link] passes through the initial points given in the problem,$\left(-2,\text{ half-dozen}\right)$

and$\left(2,\text{ 1}\right).$

The graph is an case of an exponential decay function.

Given the 2 points$\left(1,3\right)$

and$\left(\mathrm{two},\mathrm{four.5}\right),$

find the equation of the exponential function that passes through these 2 points.

$f(\mathrm{10})=\mathrm{ii}{\left(\mathrm{i.5}\right)}^{\mathrm{ten}}$

Practice two points e'er make up one's mind a unique exponential function?

*Yes, provided the two points are either both in a higher place the x-centrality or both below the x-axis and have different x-coordinates. But keep in mind that we besides need to know that the graph is, in fact, an exponential function. Not every graph that looks exponential actually is exponential. We demand to know the graph is based on a model that shows the same percent growth with each unit of measurement increase in$x,$

which in many real world cases involves time.*

Given the graph of an exponential function, write its equation.

1. First, identify ii points on the graph. Choose the y-intercept as ane of the two points whenever possible. Try to choose points that are as far apart as possible to reduce round-off mistake.
2. If one of the data points is the y-intercept $\left(0,a\right)$

   , and then

   $a$

   is the initial value. Using

   $a,$

   substitute the second point into the equation

   $f(\mathrm{10})=a{\left(b\right)}^x,$

   and solve for

   $b.$
3. If neither of the data points have the form $\left(0,a\right),$

   substitute both points into 2 equations with the form

   $f(x)=a{\left(b\right)}^x.$

   Solve the resulting arrangement of 2 equations in two unknowns to find

   $a$

   and

   $b.$
4. Write the exponential function, $f(\mathrm{ten})=a{\left(b\right)}^x.$

Writing an Exponential Function Given Its Graph

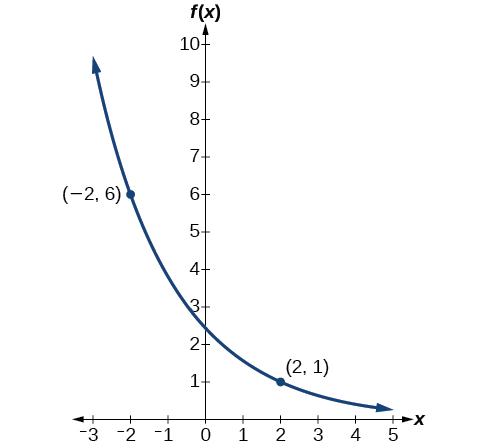
Detect an equation for the exponential function graphed in [link].

We can cull the y-intercept of the graph,$\left(0,3\right),$

as our get-go bespeak. This gives us the initial value,$a=3.$

Next, choose a signal on the curve some distance away from$\left(0,3\right)$

that has integer coordinates. One such point is$(2,12).$

$$\begin{array}{ll}y=a{b}^x\hfill & \text{Write the general form of an exponential equation}.\hfill \\ y=3b^{\mathrm{ten}}\hfill & \text{Substitute the initial value 3 for}a.\hfill \\ 12=3b^2\hfill & \text{Substitute in 12 for}y\text{ and 2 for}\mathrm{ten}.\hfill \\ 4=b^2\hfill & \text{Divide by three}.\hfill \\ b=\pm 2\begin{array}{cccc}& & & \end{array}\hfill & \text{Accept the square root}.\hfill \end{array}$$

Because we restrict ourselves to positive values of$b,$

we will utilize$b=2.$

Substitute$a$

and$b$

into the standard form to yield the equation$f(\mathrm{10})=3{(\mathrm{ii})}^x.$

Discover an equation for the exponential function graphed in [link].

$f(x)=\sqrt{\mathrm{ii}}{\left(\sqrt{2}\right)}^{\mathrm{ten}}.$

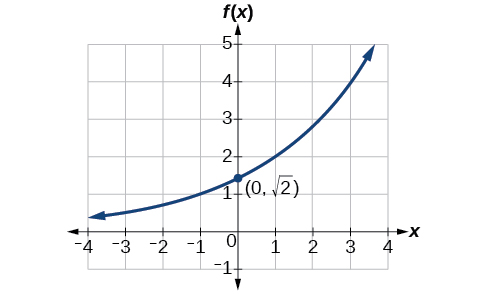
Answers may vary due to round-off error. The reply should be very close to$\mathrm{one.4142}{\left(\mathrm{one.4142}\right)}^{\mathrm{ten}}.$

Given two points on the curve of an exponential part, use a graphing reckoner to find the equation.

1. Printing [STAT].
2. Clear whatsoever existing entries in columns L1 or L2.
3. In L1, enter the ten-coordinates given.
4. In L2, enter the corresponding y-coordinates.
5. Press [STAT] again. Cursor right to CALC, scroll downwards to ExpReg (Exponential Regression), and printing [ENTER].
6. The screen displays the values of a and b in the exponential equation $y=a\cdot b^x$

   .

Using a Graphing Calculator to Find an Exponential Role

Use a graphing estimator to find the exponential equation that includes the points$(\mathrm{two},24.8)$

and$(5,198.4).$

Follow the guidelines above. First press [STAT], [EDIT], [1: Edit…], and clear the lists L1 and L2. Next, in the L1 cavalcade, enter the x-coordinates, 2 and v. Do the same in the L2 cavalcade for the y-coordinates, 24.eight and 198.4.

Now press [STAT], [CALC], [0: ExpReg] and printing [ENTER]. The values$a=6.2$

and$b=\mathrm{two}$

will exist displayed. The exponential equation is$y=\mathrm{6.ii}\cdot {\mathrm{two}}^{\mathrm{ten}}.$

Use a graphing reckoner to discover the exponential equation that includes the points (iii, 75.98) and (six, 481.07).

$y\approx 12\cdot {\mathrm{one.85}}^x$

Applying the Compound-Interest Formula

Savings instruments in which earnings are continually reinvested, such as mutual funds and retirement accounts, utilize compound involvement. The term compounding refers to interest earned not but on the original value, but on the accumulated value of the business relationship.

The annual percentage rate (April) of an account, likewise called the nominal rate, is the yearly interest rate earned by an investment account. The termnominal is used when the compounding occurs a number of times other than once per year. In fact, when interest is compounded more than than in one case a year, the effective interest charge per unit ends up beingness greater than the nominal rate! This is a powerful tool for investing.

We tin can calculate the compound interest using the compound interest formula, which is an exponential function of the variables time$t,$

principal$P,$

Apr$r,$

and number of compounding periods in a year$n:$

$$A(t)=P{\left(\mathrm{ane}+\frac{r}{n}\right)}^{nt}$$

For case, observe [link], which shows the result of investing $ane,000 at 10% for one year. Notice how the value of the account increases equally the compounding frequency increases.

Frequency	Value afterwards i year
Annually	$1100
Semiannually	$1102.50
Quarterly	$1103.81
Monthly	$1104.71
Daily	$1105.xvi

The Chemical compound Interest Formula

Chemical compound interest tin can be calculated using the formula

$A(t)=P{\left(1+\frac{r}{n}\right)}^{\mathrm{north}t}$

where

• $A(t)$

  is the account value,

• $t$

  is measured in years,

• $P$

  is the starting amount of the business relationship, often chosen the master, or more generally present value,

• $r$

  is the annual percentage charge per unit (APR) expressed as a decimal, and

• $n$

  is the number of compounding periods in ane year.

Calculating Compound Involvement

If we invest $iii,000 in an investment account paying 3% interest compounded quarterly, how much will the account be worth in 10 years?

Because we are starting with $3,000,$P=3000.$

Our interest rate is 3%, and then$r=\mathrm{0.03.}$

Because we are compounding quarterly, we are compounding 4 times per year, so$n=4.$

We desire to know the value of the business relationship in ten years, and so we are looking for$A\left(10\right),$

the value when$t=10.$

$$\begin{array}{lll}A(t)\hfill & =P{\left(\mathrm{i}+\frac{r}{\mathrm{northward}}\right)}^{nt}\hfill & \text{Use the compound involvement formula}.\hfill \\ A(\mathrm{x})\hfill & =3000{\left(1+\frac{0.03}{4}\right)}^{\mathrm{4\cdot 10}}\begin{array}{cccc}& & & \end{array}\hfill & \text{Substitute using given values}.\hfill \\ \hfill & \approx \text{\$}4045.05\hfill & \text{Round to two decimal places}.\hfill \end{array}$$

The account will be worth about $4,045.05 in ten years.

An initial investment of $100,000 at 12% interest is compounded weekly (use 52 weeks in a year). What will the investment exist worth in 30 years?

about $3,644,675.88

Using the Chemical compound Interest Formula to Solve for the Main

A 529 Program is a college-savings plan that allows relatives to invest money to pay for a kid's futurity college tuition; the account grows taxation-costless. Lily wants to set a 529 account for her new granddaughter and wants the account to grow to $xl,000 over 18 years. She believes the account will earn 6% compounded semi-annually (twice a year). To the nearest dollar, how much volition Lily need to invest in the business relationship now?

The nominal involvement rate is half dozen%, so$r=\mathrm{0.06.}$

Involvement is compounded twice a yr, so$k=2.$

Nosotros want to find the initial investment,$P,$

needed then that the value of the account will be worth $forty,000 in$18$

years. Substitute the given values into the compound interest formula, and solve for$P.$

$$\begin{array}{lll}A(t)\hfill & =P{\left(1+\frac{r}{n}\right)}^{\mathrm{north}t}\hfill & \text{Utilize the compound interest formula}.\hfill \\ \mathrm{40,000}\hfill & =P{\left(\mathrm{ane}+\frac{0.06}{2}\right)}^{2(18)}\begin{array}{cccc}& & & \end{array}\hfill & \text{Substitute using given values}A\text{,}r,n\text{, and}t.\hfill \\ \mathrm{40,000}\hfill & =P{(\mathrm{ane.03})}^{36}\hfill & \text{Simplify}.\hfill \\ \frac{\mathrm{40,000}}{{(\mathrm{one.03})}^{36}}\hfill & =P\hfill & \text{Isolate}P.\hfill \\ P\hfill & \approx \text{\$}13,801\hfill & \text{Carve up and round to the nearest dollar}.\hfill \end{array}$$

Lily will need to invest $13,801 to have $40,000 in 18 years.

Refer to [link]. To the nearest dollar, how much would Lily need to invest if the account is compounded quarterly?

$13,693

Evaluating Functions with Base e

As we saw earlier, the amount earned on an account increases as the compounding frequency increases. [link] shows that the increase from annual to semi-annual compounding is larger than the increase from monthly to daily compounding. This might lead us to enquire whether this pattern volition continue.

Examine the value of $1 invested at 100% interest for 1 year, compounded at various frequencies, listed in [link].

Frequency	$A(t)={\left(\mathrm{one}+\frac{\mathrm{one}}{\mathrm{northward}}\right)}^{\mathrm{north}}$	Value
Annually	${\left(\mathrm{one}+\frac{1}{\mathrm{ane}}\right)}^1$	$2
Semiannually	${\left(1+\frac{1}{\mathrm{ii}}\right)}^{\mathrm{two}}$	$2.25
Quarterly	${\left(\mathrm{one}+\frac{\mathrm{one}}{4}\right)}^{\mathrm{iv}}$	$2.441406
Monthly	${\left(\mathrm{ane}+\frac{\mathrm{i}}{12}\right)}^{12}$	$2.613035
Daily	${\left(1+\frac{1}{365}\right)}^{365}$	$two.714567
Hourly	${\left(1+\frac{\mathrm{one}}{\text{8760}}\right)}^{\text{8760}}$	$two.718127
Once per infinitesimal	${\left(\mathrm{i}+\frac{1}{\text{525600}}\right)}^{\text{525600}}$	$2.718279
Once per 2d	${\left(1+\frac{1}{31536000}\right)}^{31536000}$	$2.718282

These values appear to exist approaching a limit as$\mathrm{north}$

increases without bound. In fact, equally$\mathrm{northward}$

gets larger and larger, the expression${\left(1+\frac{\mathrm{i}}{\mathrm{northward}}\right)}^n$

approaches a number used and so frequently in mathematics that information technology has its own proper noun: the letter of the alphabet$\mathrm{due\; east}.$

This value is an irrational number, which means that its decimal expansion goes on forever without repeating. Its approximation to six decimal places is shown below.

The Number *east*

The letter e represents the irrational number

${\left(1+\frac{1}{\mathrm{north}}\right)}^{\mathrm{northward}},\text{as}n\text{increases without bound}$

The letter e is used as a base of operations for many real-world exponential models. To piece of work with base e, we employ the approximation,$e\approx \mathrm{two.718282.}$

The constant was named by the Swiss mathematician Leonhard Euler (1707–1783) who first investigated and discovered many of its backdrop.

Using a Computer to Detect Powers of *e*

Calculate${\mathrm{eastward}}^{3.14}.$

Circular to five decimal places.

On a calculator, press the push labeled$\left[{\mathrm{east}}^{\mathrm{ten}}\right].$

The window shows$\left[e^(\right].$

Type$\mathrm{three.14}$

and then shut parenthesis,$[)].$

Printing [ENTER]. Rounding to$\mathrm{five}$

decimal places,$e^{\mathrm{3.xiv}}\approx \mathrm{23.10387.}$

Circumspection: Many scientific calculators have an "Exp" button, which is used to enter numbers in scientific annotation. It is not used to discover powers of$e.$

Utilize a figurer to find$e^{-\mathrm{0.five}}.$

Round to v decimal places.

$e^{-0.5}\approx 0.60653$

Investigating Continuous Growth

So far we accept worked with rational bases for exponential functions. For most real-world phenomena, notwithstanding, due east is used every bit the base of operations for exponential functions. Exponential models that utilise$\mathrm{due\; east}$

as the base are called continuous growth or disuse models. We see these models in finance, calculator scientific discipline, and almost of the sciences, such every bit physics, toxicology, and fluid dynamics.

The Continuous Growth/Decay Formula

For all real numbers$t,$

and all positive numbers$a$

and$r,$

continuous growth or decay is represented past the formula

$$A(t)=a{\mathrm{east}}^{rt}$$

where

• $a$

  is the initial value,

• $r$

  is the continuous growth rate per unit time,

• and $t$

  is the elapsed time.

If$r>0$

, then the formula represents continuous growth. If$r<0$

, then the formula represents continuous decay.

For business applications, the continuous growth formula is called the continuous compounding formula and takes the class

$$A(t)=P{e}^{rt}$$

where

• $P$

  is the principal or the initial invested,

• $r$

  is the growth or interest rate per unit time,

• and $t$

  is the flow or term of the investment.

**Given the initial value, rate of growth or decay, and time$t,$

solve a continuous growth or decay function.**

1. Use the information in the problem to decide $a$

   , the initial value of the office.

2. Use the data in the problem to determine the growth rate $r.$
   1. If the problem refers to continuous growth, and so $r>0.$
   2. If the problem refers to continuous decay, then $r<0.$
3. Employ the information in the problem to determine the time $t.$
4. Substitute the given data into the continuous growth formula and solve for $A(t).$

Calculating Continuous Growth

A person invested $1,000 in an account earning a nominal 10% per year compounded continuously. How much was in the business relationship at the end of i year?

Since the business relationship is growing in value, this is a continuous compounding trouble with growth rate$r=\mathrm{0.10.}$

The initial investment was $1,000, then$P=1000.$

We use the continuous compounding formula to observe the value after$t=\mathrm{ane}$

year:

$$\begin{array}{lll}A(t)\hfill & =P{\mathrm{due\; east}}^{rt}\hfill & \text{Use the continuous compounding formula}.\hfill \\ \hfill & =\mathrm{grand}{(e)}^{0.1}\begin{array}{cccc}& & & \end{array}\hfill & \text{Substitute known values for}P,r,\text{ and}t.\hfill \\ \hfill & \approx 1105.17\hfill & \text{Apply a figurer to guess}.\hfill \end{array}$$

The account is worth $1,105.17 after 1 year.

A person invests $100,000 at a nominal 12% interest per yr compounded continuously. What will be the value of the investment in xxx years?

$3,659,823.44

Computing Continuous Decay

Radon-222 decays at a continuous rate of 17.3% per twenty-four hours. How much will 100 mg of Radon-222 decay to in 3 days?

Since the substance is decaying, the rate,$17.3\%$

, is negative. So,$r=-\mathrm{0.173.}$

The initial amount of radon-222 was$100$

mg, and so$a=100.$

Nosotros use the continuous decay formula to discover the value after$t=\mathrm{iii}$

days:

$$\begin{array}{lll}A(t)\hfill & =a{\mathrm{east}}^{rt}\hfill & \text{Use the continuous growth formula}.\hfill \\ \hfill & =100{\mathrm{due\; east}}^{-0.173(\mathrm{three})}\begin{array}{cccc}& & & \end{array}\hfill & \text{Substitute known values for}a,r,\text{ and}t.\hfill \\ \hfill & \approx 59.5115\hfill & \text{Use a calculator to guess}.\hfill \end{array}$$

So 59.5115 mg of radon-222 will remain.

Using the data in [link], how much radon-222 will remain afterward one twelvemonth?

three.77E-26 (This is calculator notation for the number written equally$3.77\times {\mathrm{ten}}^{-26}$

in scientific notation. While the output of an exponential function is never zero, this number is and then shut to zero that for all practical purposes nosotros tin can accept zero as the answer.)

Key Equations

definition of the exponential role	$f(\mathrm{ten})=b^{\mathrm{ten}}\text{, where}b>0,b\ne 1$
definition of exponential growth	$f(x)=a{b}^x,\text{ where}a>0,b>0,b\ne 1$
compound interest formula	$\begin{array}{l}A(t)=P{\left(\mathrm{ane}+\frac{r}{n}\right)}^{nt},\text{ where}\hfill \\ A(t)\text{ is the account value at fourth dimension}t\hfill \\ t\text{ is the number of years}\hfill \\ P\text{ is the initial investment, often called the principal}\hfill \\ r\text{ is the annual percentage rate (APR), or nominal rate}\hfill \\ n\text{ is the number of compounding periods in one twelvemonth}\hfill \end{array}$
continuous growth formula	$A(t)=a{e}^{rt},\text{ where}$ $t$is the number of unit time periods of growth $a$is the starting amount (in the continuous compounding formula a is replaced with P, the master) $e$is the mathematical constant,$\mathrm{east}\approx 2.718282$

Key Concepts

• An exponential office is divers as a function with a positive abiding other than $1$

  raised to a variable exponent. See [link].

• A function is evaluated past solving at a specific value. Encounter [link] and [link].
• An exponential model can be plant when the growth rate and initial value are known. Run into [link].
• An exponential model can be found when the two data points from the model are known. Run into [link].
• An exponential model can be found using two data points from the graph of the model. Meet [link].
• An exponential model tin be found using two data points from the graph and a reckoner. See [link].
• The value of an account at whatsoever time $t$

  tin be calculated using the compound interest formula when the primary, annual interest rate, and compounding periods are known. See [link].

• The initial investment of an business relationship can be institute using the chemical compound interest formula when the value of the business relationship, almanac interest rate, compounding periods, and life span of the account are known. See [link].
• The number $\mathrm{eastward}$

  is a mathematical abiding often used every bit the base of operations of existent world exponential growth and decay models. Its decimal approximation is

  $e\approx \mathrm{ii.718282.}$
• Scientific and graphing calculators have the fundamental $\left[{\mathrm{due\; east}}^x\right]$

  or

  $\left[\exp (\mathrm{10})\right]$

  for calculating powers of

  $\mathrm{due\; east}.$

  Run across [link].

• Continuous growth or decay models are exponential models that use $e$

  as the base. Continuous growth and decay models can be found when the initial value and growth or decay rate are known. See [link] and [link].

Section Exercises

Verbal

Explicate why the values of an increasing exponential function will eventually overtake the values of an increasing linear function.

Linear functions have a constant rate of change. Exponential functions increase based on a percent of the original.

Given a formula for an exponential office, is it possible to decide whether the function grows or decays exponentially merely by looking at the formula? Explicate.

The Oxford Dictionary defines the word nominal as a value that is "stated or expressed but not necessarily corresponding exactly to the real value."² Develop a reasonable argument for why the term nominal rate is used to describe the annual percentage rate of an investment account that compounds interest.

When interest is compounded, the pct of interest earned to principal ends up being greater than the annual percentage rate for the investment business relationship. Thus, the annual percentage charge per unit does not necessarily correspond to the real interest earned, which is the very definition of nominal.

Algebraic

For the following exercises, place whether the statement represents an exponential function. Explain.

The average annual population increase of a pack of wolves is 25.

A population of bacteria decreases by a factor of$\frac{\mathrm{ane}}{8}$

every$24$

hours.

exponential; the population decreases by a proportional charge per unit. .

The value of a coin collection has increased by$3.25\%$

annually over the last$20$

years.

For each training session, a personal trainer charges his clients$\text{\$}5$

less than the previous training session.

not exponential; the charge decreases past a constant amount each visit, and so the argument represents a linear function. .

The summit of a projectile at time$t$

is represented by the role$h(t)=-\mathrm{iv.9}{t}^2+18t+40.$

For the following exercises, consider this scenario: For each twelvemonth$t,$

the population of a forest of trees is represented past the function$A(t)=115{(\mathrm{one.025})}^t.$

In a neighboring wood, the population of the aforementioned type of tree is represented past the function$B(t)=82{(1.029)}^t.$

(Round answers to the nearest whole number.)

Which forest's population is growing at a faster rate?

The forest represented by the role$B(t)=82{(1.029)}^t.$

Which wood had a greater number of trees initially? By how many?

Assuming the population growth models continue to correspond the growth of the forests, which forest will have a greater number of trees after$\mathrm{twenty}$

years? By how many?

After$t=20$

years, forest A will have$43$

more trees than woods B.

Assuming the population growth models continue to correspond the growth of the forests, which forest will have a greater number of trees later on$100$

years? By how many?

Discuss the above results from the previous iv exercises. Assuming the population growth models keep to represent the growth of the forests, which wood will have the greater number of trees in the long run? Why? What are some factors that might influence the long-term validity of the exponential growth model?

Answers will vary. Sample response: For a number of years, the population of wood A will increasingly exceed forest B, but because forest B actually grows at a faster rate, the population volition eventually go larger than woods A and will remain that way as long every bit the population growth models concur. Some factors that might influence the long-term validity of the exponential growth model are drought, an epidemic that culls the population, and other environmental and biological factors.

For the following exercises, decide whether the equation represents exponential growth, exponential decay, or neither. Explain.

$y=220{\left(1.06\right)}^x$

exponential growth; The growth factor,$1.06,$

is greater than$\mathrm{ane.}$

$y=\mathrm{eleven},701{\left(0.97\right)}^t$

exponential decay; The decay factor,$0.97,$

is between$0$

and$1.$

For the post-obit exercises, notice the formula for an exponential function that passes through the two points given.

$\left(-1,\frac{3}{2}\right)$

and$\left(3,24\right)$

$f(\mathrm{10})={\left(\frac{\mathrm{one}}{\mathrm{vi}}\right)}^{-\frac{3}{\mathrm{five}}}{\left(\frac{1}{6}\right)}^{\frac{x}{5}}\approx 2.93{\left(0.699\right)}^{\mathrm{ten}}$

For the post-obit exercises, make up one's mind whether the table could represent a function that is linear, exponential, or neither. If information technology appears to exist exponential, detect a function that passes through the points.

| $$

x

</math></strong> | 1 | 2 | three | four | | $$

f ( x )

</math></strong> | seventy | xl | 10 | -20 |

Linear

| $$

x

</math></strong> | i | 2 | three | iv | | $$

h ( x )

</math></strong> | 70 | 49 | 34.3 | 24.01 |

| $$

x

</math></strong> | 1 | 2 | three | 4 | | $$

yard ( x )

</math></strong> | 80 | 61 | 42.ix | 25.61 |

Neither

$x$	1	ii	3	4
$f(x)$	x	20	forty	lxxx

| $$

x

</math></potent> | i | 2 | 3 | four | | $$

thousand ( ten )

</math></strong> | -3.25 | 2 | 7.25 | 12.5 |

Linear

For the following exercises, use the compound interest formula,$A(t)=P{\left(\mathrm{one}+\frac{r}{\mathrm{north}}\right)}^{\mathrm{north}t}.$

Later on a certain number of years, the value of an investment account is represented by the equation$10,250{\left(1+\frac{0.04}{12}\right)}^{120}.$

What is the value of the account?

What was the initial deposit made to the account in the previous practice?

$\$\mathrm{x},250$

How many years had the account from the previous exercise been accumulating interest?

An business relationship is opened with an initial deposit of $6,500 and earns$\mathrm{iii.half-dozen}\%$

interest compounded semi-annually. What will the business relationship be worth in$\mathrm{xx}$

years?

$\$\mathrm{xiii},268.58$

How much more would the business relationship in the previous exercise have been worth if the involvement were compounding weekly?

Solve the compound interest formula for the chief,$P$

.

$P=A(t)\cdot {\left(1+\frac{r}{n}\right)}^{-nt}$

Use the formula plant in the previous exercise to calculate the initial deposit of an business relationship that is worth$\$\mathrm{fourteen},472.74$

subsequently earning$5.5\%$

interest compounded monthly for$\mathrm{five}$

years. (Round to the nearest dollar.)

How much more would the account in the previous two exercises exist worth if information technology were earning interest for$5$

more years?

$\$\mathrm{4,572.56}$

Use properties of rational exponents to solve the compound interest formula for the interest rate,$r.$

Utilise the formula institute in the previous exercise to calculate the interest rate for an account that was compounded semi-annually, had an initial deposit of $9,000 and was worth $thirteen,373.53 after 10 years.

$4\%$

Use the formula found in the previous exercise to calculate the involvement rate for an account that was compounded monthly, had an initial deposit of $five,500, and was worth $38,455 later on 30 years.

For the post-obit exercises, determine whether the equation represents continuous growth, continuous decay, or neither. Explain.

$y=3742{\left(\mathrm{due\; east}\right)}^{0.75t}$

continuous growth; the growth rate is greater than$0.$

$y=\mathrm{two.25}{\left(e\right)}^{-\mathrm{ii}t}$

continuous decay; the growth rate is less than$0.$

Suppose an investment account is opened with an initial deposit of$\$12,000$

earning$7.2\%$

involvement compounded continuously. How much will the account be worth subsequently$\mathrm{xxx}$

years?

How much less would the account from Exercise 42 exist worth later on$30$

years if it were compounded monthly instead?

$\$669.42$

Numeric

For the following exercises, evaluate each function. Circular answers to four decimal places, if necessary.

$f(\mathrm{ten})=2{\left(5\right)}^{\mathrm{10}},$

for$f\left(-3\right)$

$f(\mathrm{10})=-4^{2\mathrm{10}+3},$

for$f\left(-\mathrm{i}\right)$

$f(-\mathrm{ane})=-\mathrm{iv}$

$f(x)=-2e^{x-1},$

for$f\left(-\mathrm{ane}\right)$

$f(-1)\approx -0.2707$

$f(x)=2.7{\left(\mathrm{iv}\right)}^{-\mathrm{ten}+\mathrm{one}}+1.5,$

for$f\left(-2\right)$

$f(x)=\mathrm{one.2}{\mathrm{eastward}}^{\mathrm{ii}x}-0.3,$

for$f\left(3\right)$

$f(\mathrm{three})\approx 483.8146$

$f(x)=-\frac{\mathrm{three}}{2}{\left(\mathrm{iii}\right)}^{-\mathrm{ten}}+\frac{3}{2},$

for$f\left(2\right)$

Technology

For the following exercises, use a graphing calculator to find the equation of an exponential function given the points on the curve.

$(\mathrm{three},222.62)$

and$(\mathrm{ten},77.456)$

$(20,29.495)$

and$(150,730.89)$

$y\approx 18\cdot {1.025}^x$

$(5,2.909)$

and$(\mathrm{xiii},0.005)$

$(\mathrm{11,310.035})$

and $(\mathrm{25,356.3652})$

$y\approx 0.2\cdot {\mathrm{ane.95}}^x$

Extensions

The almanac percentage yield (APY) of an investment account is a representation of the actual interest rate earned on a compounding account. It is based on a compounding period of one year. Prove that the APY of an account that compounds monthly can be found with the formula$\text{APY}={\left(\mathrm{i}+\frac{r}{12}\right)}^{12}-\mathrm{i.}$

Repeat the previous practice to find the formula for the APY of an account that compounds daily. Apply the results from this and the previous exercise to develop a function$I(n)$

for the APY of whatever account that compounds$n$

times per year.

$\text{APY}=\frac{A(t)-a}{a}=\frac{a{\left(1+\frac{r}{365}\right)}^{365(\mathrm{ane})}-a}{a}=\frac{a\left[{\left(1+\frac{r}{365}\right)}^{365}-1\right]}{a}={\left(\mathrm{one}+\frac{r}{365}\right)}^{365}-1;$ $I(n)={\left(1+\frac{r}{\mathrm{north}}\right)}^n-1$

Recall that an exponential function is whatsoever equation written in the form$f(\mathrm{ten})=a\cdot b^{\mathrm{ten}}$

such that$a$

and$b$

are positive numbers and$b\ne \mathrm{one.}$

Whatsoever positive number$b$

tin can be written as$b=e^n$

for some value of$n$

. Apply this fact to rewrite the formula for an exponential function that uses the number$e$

as a base of operations.

In an exponential decay part, the base of the exponent is a value between 0 and 1. Thus, for some number$b>1,$

the exponential decay function can be written as$f(\mathrm{10})=a\cdot {\left(\frac{\mathrm{one}}{b}\right)}^x.$

Use this formula, along with the fact that$b=e^{\mathrm{northward}},$

to testify that an exponential decay part takes the grade$f(x)=a{\left(e\right)}^{-\mathrm{northward}x}$

for some positive number$n$

.

Allow$f$

be the exponential decay function$f(\mathrm{ten})=a\cdot {\left(\frac{1}{b}\right)}^{\mathrm{10}}$

such that$b>1.$

Then for some number$\mathrm{due\; north}>0,$

$f(x)=a\cdot {\left(\frac{\mathrm{ane}}{b}\right)}^{\mathrm{ten}}=a{\left(b^{-1}\right)}^x=a{\left({\left(e^n\right)}^{-\mathrm{ane}}\right)}^x=a{\left(e^{-n}\right)}^x=a{\left(\mathrm{eastward}\right)}^{-nx}.$

The formula for the corporeality$A$

in an investment account with a nominal interest rate$r$

at whatsoever time$t$

is given by$A(t)=a{\left(\mathrm{due\; east}\right)}^{rt},$

where$a$

is the amount of principal initially deposited into an business relationship that compounds continuously. Show that the percentage of interest earned to principal at any fourth dimension$t$

can be calculated with the formula$I(t)=e^{rt}-1.$

Existent-World Applications

The play a joke on population in a certain region has an annual growth rate of nine% per year. In the year 2012, there were 23,900 fox counted in the area. What is the play a trick on population predicted to be in the twelvemonth 2020?

A scientist begins with 100 milligrams of a radioactive substance that decays exponentially. Afterwards 35 hours, 50mg of the substance remains. How many milligrams will remain afterwards 54 hours?

In the twelvemonth 1985, a firm was valued at $110,000. By the twelvemonth 2005, the value had appreciated to $145,000. What was the annual growth rate between 1985 and 2005? Presume that the value continued to grow past the same pct. What was the value of the house in the yr 2010?

$1.39\%;$ $\$155,368.09$

A car was valued at $38,000 in the year 2007. By 2013, the value had depreciated to $11,000 If the motorcar'southward value continues to driblet by the same pct, what will information technology be worth by 2017?

Jamal wants to relieve $54,000 for a down payment on a home. How much will he need to invest in an account with 8.two% Apr, compounding daily, in guild to reach his goal in 5 years?

$\$35,838.76$

Kyoko has $10,000 that she wants to invest. Her bank has several investment accounts to choose from, all compounding daily. Her goal is to take $15,000 by the time she finishes graduate school in 6 years. To the nearest hundredth of a percent, what should her minimum annual involvement rate be in order to attain her goal? (Hint: solve the compound interest formula for the interest charge per unit.)

Alyssa opened a retirement business relationship with vii.25% Apr in the year 2000. Her initial deposit was $13,500. How much will the account exist worth in 2025 if interest compounds monthly? How much more would she make if involvement compounded continuously?

$\$82,247.78;$ $\$449.75$

An investment account with an annual interest charge per unit of vii% was opened with an initial deposit of $four,000 Compare the values of the account after 9 years when the interest is compounded annually, quarterly, monthly, and continuously.

Footnotes

• one http://world wide web.worldometers.info/earth-population/. Accessed February 24, 2014.
• 2 Oxford Dictionary. http://oxforddictionaries.com/us/definition/american\_english/nomina.

Glossary

annual percent rate (April)

the yearly interest charge per unit earned by an investment business relationship, also called nominal rate

chemical compound interest

interest earned on the total balance, not but the principal

exponential growth

a model that grows by a rate proportional to the amount present

nominal rate

the yearly interest rate earned by an investment account, also called annual percent rate

---

This work is licensed under a Creative Commons Attribution iv.0 International License.

You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1

Attribution:

• For questions regarding this license, delight contact partners@openstaxcollege.org.
• If y'all use this textbook every bit a bibliographic reference, then you should cite it every bit follows: OpenStax College, Precalculus. OpenStax CNX. http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.i.
• If you redistribute this textbook in a print format, then you must include on every physical folio the following attribution: "Download for gratuitous at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@eight.1."
• If you redistribute office of this textbook, then you must retain in every digital format folio view (including but not express to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1."

Source: https://philschatz.com/precalculus-book/contents/m49361.html

Posted by: hilljusture1993.blogspot.com

Share this post